大模型训练推理资源与计算量评估

计算量评估

前馈神经网络计算量

前馈神经网络：Y = XW +B

在这个过程中，完成的运算如下：

$$ \begin{bmatrix} x_0 & x_1 & x_2 \end{bmatrix} \times \begin{bmatrix} w_{00} & w_{01} \ w_{10} & w_{11} \ w_{20} & w_{21} \end{bmatrix} + \begin{bmatrix} b_0 \ b_1 \end{bmatrix} $$

其中，W是权重矩阵，X是输入向量，B是偏置项。即：

$$ y = \begin{bmatrix} y_0 \ y_1 \end{bmatrix} \begin{matrix} y_0 = w_{00}x_0 + w_{01}x_1 + b_0\ y_1 = w_{10}x_0 + w_{11}x_1 + b_1\
\end{matrix} $$

上述2个公式中，每个公式都有3个加法、3个乘法计算。所以[1,3]的矩阵和[3,2]的矩阵相乘共包含 2132 =12 次浮点计算量(称为FLOPs)。从而推广到一般：[m,k]的矩阵和[k,n]的矩阵相乘，需要2mkn FLOPs。而GPU在不同精度单位下，浮点数运算的效率是不同的。例如，A100在16位精度(FP16或BF16)下每秒可以进行$31410^{12}$次浮点运算。而在32位精度下，每秒只能进行$15610^{12}$次浮点运算。所以，我们可以理所当然的想到一个提速思路 - 让所有运算在低精度下进行来提高训练/推理效率。但是，这里有个无法忽略的问题：某些计算必须要在高精度下进行。例如全程在低精度下进行模型训练，往往会出现由于精度不够导致数值溢出和无法收敛的问题。所以目前大模型训练通常采用的是混合精度方式进行：前向传播、反向传播这些无需高精度的计算采用16位精度(FP16或BF16)进行，优化器状态更新在32位精度(FP32)进行。而模型推理的要求就比较低，可以在16位、8位甚至4位精度进行，整个任务的计算效率非常高。

模型计算量分析

$$ 训练计算量 = F_{前向传播} + F_{反向传播}\ 推理计算量 = F_{前向传播} \ F_{反向传播} = 2*F_{前向传播} $$

接下来进行$F_{前向传播}$的计算推导：

先确定符号：我们令B对应batch size，s对应sequence length，h对应hidden dimension，l对应layers number；接着，我们再来观察大模型结构：大模型本身由l个transformer块串联而成。此外，首transformer块前和尾transformer块后还有一些结构。所以大模型的算力估算可以分为两大块：一、l个transformer块中的FLOPs；二、其他结构中的FLOPs：

transformer块中，每个transformer块都由多头注意力结构和MLP两种结构构成：

多头注意力机制所需计算量：

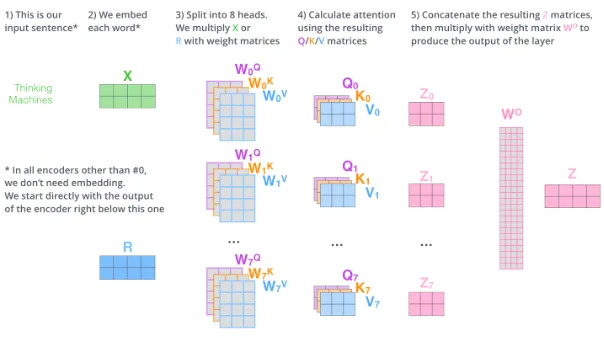
250da86b2e1b6fb734121a17b5125e55f7d9f8eac87875c3ac6ba3654b8827da

QKV计算量：

$$ Q = XW^Q, K=XW^K, V=XW^V, 其中： x \in [B,s,h], W^Q\in[h,h/a] $$

涉及计算量大致如下：

$$ 32Bshh/aa=6Bsh^2,其中a是多头注意力机制的head数。 $$

注意力计算量：<br>

注意力分数计算单头注意力分数一般采用如下计算：

$$ attention = QK^T / \sqrt(d_k) $$

计算量为：

$$ 2Bsh/a*s=2Bs^2h/a,其中Q \in [B,s,h/a], K^T \in[B,h/a,s] $$

因此多头注意力分数整体计算量：

$$ 2Bs^2h/a*a=2Bsh^2 $$

注意力输出层计算量：单头注意力输出层计算量：计算公式为：

$$ Z= attention \times V, 其中attention \in [B,s,s], V\in[B,s,h/a] $$

计算量为：

$$ 2Bss*h/a=2Bs^2h/a $$

因此多头注意力输出层计算量为：$2Bs^2h/a*a=2Bs^2h$

多头注意力合并层计算量<br> 计算公式为：

$$ y = W^OZ + B \ 其中,Z\in[B,s,h], W^O \in [h, h], Z为多头注意力输出层结果拼接 $$

计算量为：

$$ 2Bsh*h=2Bsh^2 $$

因此整个自注意力层的计算量为：

$$ 4Bs^2h+8Bsh^2 $$

MLP层所需计算量

激活值和第一个线性层相乘：$[B,s,h]*[h,4h] 共8Bsh^2$ FLOPs；
激活值和第二个线性层相乘：$[B,s,4h]*[4h,h] 共8Bsh^2$ FLOPs；
激活层为约0FLOPs：GeLU是确定的数学缩放公式，可认为无需矩阵乘；

单个MLP共有包含$16Bsh^2$$ FLOPs。<br> 因此，l个transformer块的FLOPs为：$24Bsh^2+4Bs^2h$，所有transformer块的FLOPs为：$l(24Bsh^2+4Bs^2h)$。

其他结构所需计算量

主要是最终输出层，计算公式为：

$$ y = XW^O + B, 其中X\in[B,s,h], W^O \in [h,V], V为字典大小 $$

其计算量大小为：

$$ 2Bsh*V=2BsVh $$

综上，整个模型的前向传播计算量为：

$$ F_{前向传播} = l(24Bsh^2+4Bs^2h)+2BsVh \ = 24Bsh^2l+4Bs^2hl+2BsVh \ = 24Bsh^2l(1+\frac{s}{6h}+\frac{V}{12lh}) $$

而通常在大模型中，6h远大于s，12lh远大于V，所以还可以进一步简化：

$$ F_{前向传播} = 24Bsh^2l $$

因此可推断，训练与推理所需的计算量为：

$$ F_{训练} = 3F_{前向传播} = 72Bsh^2l \ F_{训练} = 4F_{前向传播} = 96Bsh^2l,全量参数计算时 \ F_{推理} = F_{前向传播} = 24Bsh^2l $$

粗略估算一般基于transformer的大模型的参数量为$12lh^2$,可以发现： 1）模型训练中：如果没有应用激活值重计算，单模型副本处理每个tokens时，单参数上算力需求约为6FLOPs($\frac{72Bsh^2l}{12lh^2Bs}$)。如果应用全激活值重计算，提升至8FLOPs； 2）模型推理中：单模型副本处理每个tokens时，单参数上算力需求约为6FLOPs；

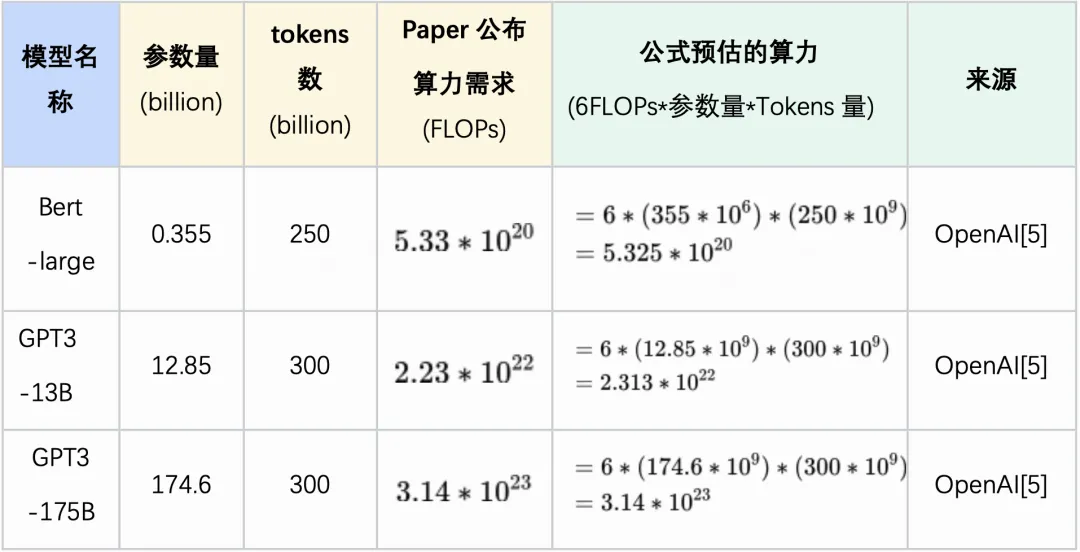
b7530fd66541fc9ea2132a8dd205a7011dda6210ab3ac10ac39d42ed4cc6c04c

最常用来测量每秒浮点运算次数的基准程序（benchmark）之一，就是Linpack。一个MFLOPS（megaFLOPS）等于每秒一百万（=10^6）次的浮点运算，一个GFLOPS（gigaFLOPS）等于每秒十亿（=10^9）次的浮点运算，一个TFLOPS（teraFLOPS）等于每秒一万亿（=10^12）次的浮点运算，一个PFLOPS（petaFLOPS）等于每秒一千万亿（=10^15）次的浮点运算，一个EFLOPS（exaFLOPS）等于每秒一百亿亿（=10^18）次的浮点运算。

模型训练时间估算

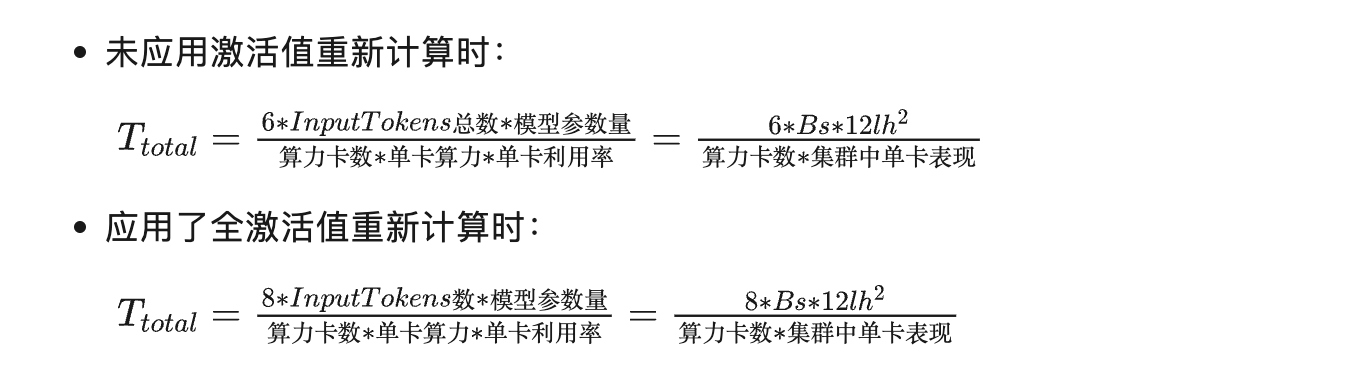
根据阿姆达尔定律，由于整个系统中有网络通信等无法并行加速项的存在，集群中存在加速比上限。通常，训练集群中的GPU利用率通常约30%～55%之间。集群训练耗时计算公式如下： c3b91e8f5a779118ff3f119f3152c5aec3f0bc54e4712e757a9e828bdd53d74b

https://blog.csdn.net/weixin_43925843/article/details/145626893 https://www.nvidia.cn/data-center/v100/ f048f9cb18ca409edeeb27e838ce9a011cf21bd80c82afa9ff3ca00fa33136ee https://github.com/hiyouga/LLaMA-Factory/blob/main/README_zh.md#%E8%BD%AF%E7%A1%AC%E4%BB%B6%E4%BE%9D%E8%B5%96

LLaMA Factory 微调所需的硬件资源计算主要基于模型参数量、微调方法和训练配置三个核心维度。以下是具体计算方法与典型场景示例：

一、显存需求计算公式

显存占用（GB）主要包含以下部分：

$$ \text{显存} = \text{模型参数显存} + \text{梯度显存} + \text{优化器状态显存} + \text{激活值显存} $$

1. 模型参数显存

全参数微调（FP16）：参数量 × 2 bytes（例如 7B 模型：7×10⁹ × 2 / 10⁹ = 14GB）
LoRA（FP16）：仅需存储低秩矩阵（约 0.1%-1% 参数量）（例如 7B 模型：14GB × 1% ≈ 0.14GB）
QLoRA（4-bit）：参数量 × 0.5 bytes （例如 7B 模型：7×10⁹ × 0.5 / 10⁹ = 3.5GB）

2. 梯度与优化器状态

全参数微调（Adam优化器）：参数量 × 4 bytes（梯度+优化器状态）
LoRA/QLoRA：仅需存储少量梯度（可忽略）

3. 激活值显存 与批次大小（batch size）和序列长度（seq_len）相关，计算公式：

$$ \text{激活值显存} \approx \text{batch_size} \times \text{seq_len} \times \text{hidden_dim} \times 2 \text{ bytes} $$

二、典型场景硬件需求

模型规模	微调方法	显存需求（估算）	推荐 GPU 配置
7B	全参数（FP16）	60GB	2×A100 80GB
7B	QLoRA（4-bit）	6GB	单卡 RTX 3090/4090
13B	LoRA（FP16）	12GB	单卡 A100 40GB
70B	全参数（FP16）	600GB	8×H100 80GB（NVLink）

三、关键影响因素

微调算法选择
- 全参数微调：显存需求最高，适合高算力集群。
- LoRA/QLoRA：显存需求降低 50%-90%，适合单卡训练。
- GaLore/Freeze：通过梯度压缩或参数冻结进一步优化显存。
训练配置优化
- 批次大小（batch_size）：增大 batch_size 会线性增加激活值显存。
- 梯度累积（gradient_accumulation）：通过累积梯度减少单步显存需求。
- 量化与混合精度：4-bit/8-bit 量化可降低显存 30%-70%。
分布式训练支持 LLaMA Factory 支持 DeepSpeed ZeRO 和模型并行，可将大模型拆分到多卡。

四、实战示例（7B模型 + QLoRA）

硬件配置：RTX 4090（24GB 显存）

训练命令：

1
2
3
4
5
6


llamafactory-cli train \
  --model_name_or_path meta-llama/Llama-3-8b \
  --finetuning_type qlora \
  --quantization_bit 4 \
  --per_device_train_batch_size 4 \
  --gradient_accumulation_steps 8

显存占用：约 10-12GB（含激活值）。

五、资源估算工具

LLaMA Factory 提供显存估算工具，可通过以下命令生成报告：

1

llamafactory-cli estimate --model_name_or_path meta-llama/Llama-3-8b --finetuning_type lora

如需更精确的计算，可参考 Hugging Face 的 Transformer 显存计算器。 https://mp.weixin.qq.com/s/CJxA-PxF_lvSpMr_7uHVVg

推理所用显存： Total GPU Memory = 模型大小 + KV Cache + Memory Overhead 最后还是以 LLaMa-2 13B 来举例。假设有 10 个并发请求，同时请求 LLaMa-2 13B 以最大 Token数(4096) 进行模型推理。那最终需要的 GPU Memory 计算过程如下：模型大小= 13 Billion * 2 Bytes = 26 GB

Total KV cache= 800 KB * 4096 Tokens * 10 并发请求 = 32 GB

Memory Overhead= 0.1 * (26 GB + 32 GB) = 5.8 GB

所以最终需要总 GPU memory为: 26 GB + 32 GB + 5.8 GB = 63.8 GB。需要 2 块英伟达的 A100 芯片才可以。 https://github.com/manuelescobar-dev/LLM-Tools

https://medium.com/@manuelescobar-dev/memory-requirements-for-llm-training-and-inference-97e4ab08091b

显存计算

推理显存评估：

$$ Total\ Inference\ Memory = Model Size + KV Cache + Activations $$

模型大小：

e21334b55e5c3e6692bf0d25103d42c561d602963061639d2981a314a86b2838

kv cache：

$$ KV\ Cache =2 × Batch Size × Sequence Length × Number of Layers × Hidden Size × Precision $$

激活值：

$$ Activation Memory = Batch Size × Sequence Length × Hidden Size × ( 34 + 5 × \frac{Sequence Length ×Number of attention heads}{Hidden Size}) $$

推理显存评估：

$$ Total Memory=Model Size+KV Cache+Activations+(Optimizer States+Gradients)× Number of Trainable Parameters $$

Optimizer States Optimization algorithms require resources to store the parameters and auxiliary variables. These variables include momentum and variance used by algorithms such as Adam (2 states) or SGD (1 state). The precision and type of optimizer affect memory usage.

Formula [1]

AdamW (2 states): 8 Bytes per parameter AdamW (bitsandbytes Quantized): 2 Bytes per parameter SGD (1 state): 4 Bytes per parameter Gradients Gradient values are computed during the backward pass of the model. They represent the rate of change of the loss function with respect to each model parameter and are crucial for updating the parameters during optimization. As with activations, they must be stored in FP32 for numerical stability.

Formula [1]

4 Bytes per parameter