机器学习概述

AI vs ML vs DL

AI:人工智能

人工智能是在1956年达特茅斯会议上首先提出的。该会议确定了人工智能的目标是“实现能够像人类一样利用知识去解决问题的机器”。

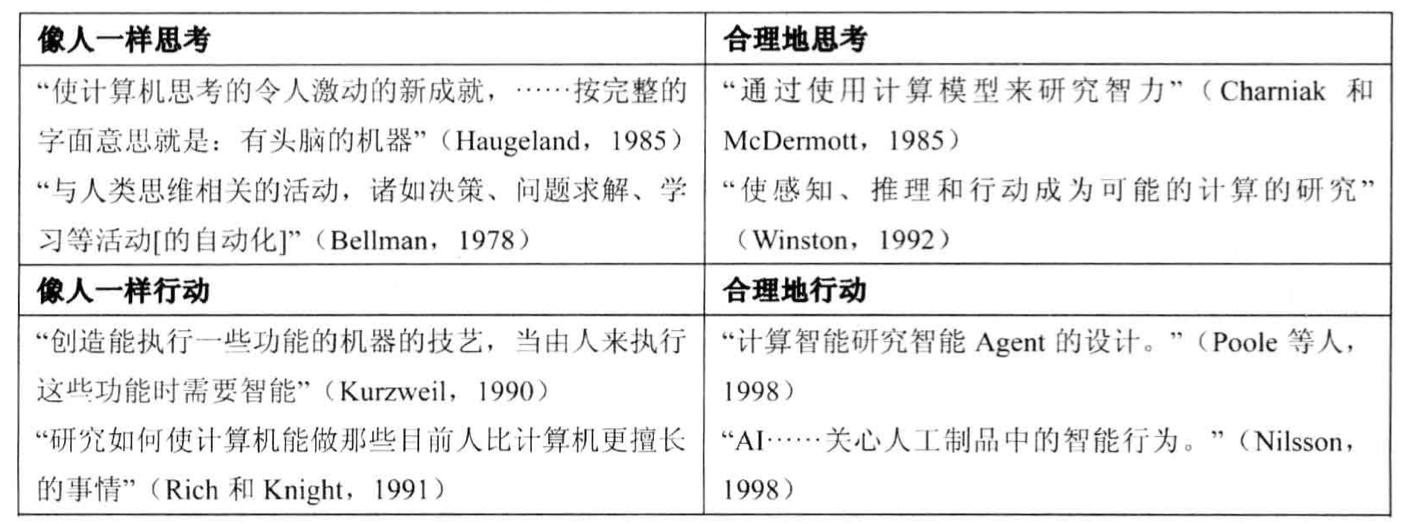
像人一样思考：认知科学

像人一样行动：图灵测试（1950）的途径

自然语言处理
知识表示
自动推理
机器学习

完全图灵测试：

计算视觉
机器人学

合理地思考：逻辑学

合理地行动：强化学习

机器学习

学习的定义：

Herbert A. Simon：如果一个系统能够通过执行某个过程改进他的性能，这就是学习。

Tom M. Mitchell：

Study of algorithms that

improve their performance P
at some task T
withexperience E

well-defined learning task: <P,T,E> 一个程序被认为能从经验E中学习，解决任务 T，达到性能度量值P，当且仅当，有了经验E后，经过P评判，程序在处理 T 时的性能有所提升。

机器学习：从原始数据中获取模式(规律)

深度学习

表示学习：自动地学习出有效特征, 并最终提升机器学习模型性能的方法。

局部学习：0ne-hot编码

分布表示：连续表示（RGB）、词向量（词嵌入）

特征工程 VS 表示学习：

特征工程：人工提取特征

表示学习：自动获取特征

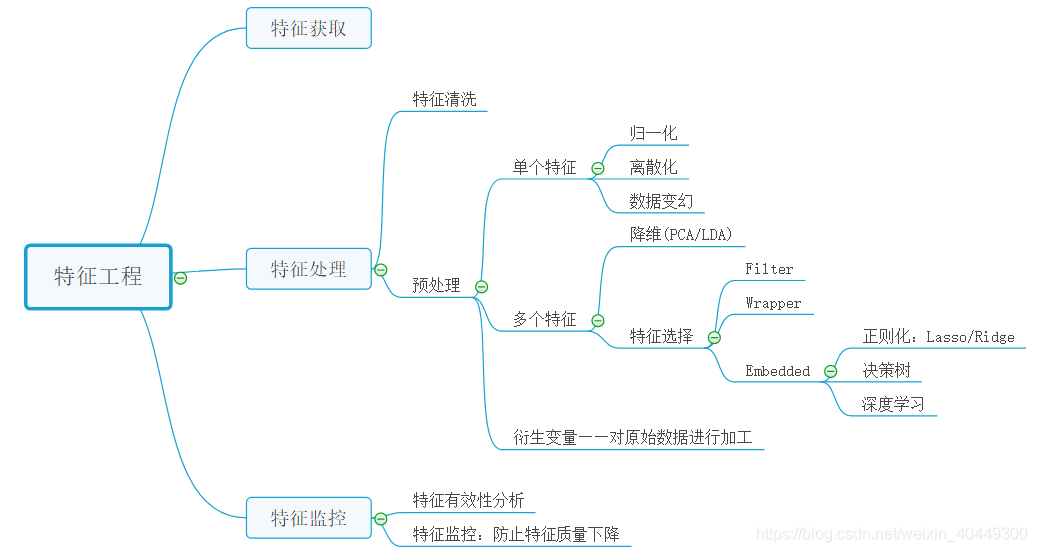
深度学习：

统计学 vs 统计学习 vs 机器学习

参考文献：http://brenocon.com/blog/2008/12/statistics-vs-machine-learning-fight/

统计学：Statistics

统计学习：Statistical learning

统计机器学习:Statistical machine learning

机器学习：Machine Learning

机器学习 vs 数据挖掘

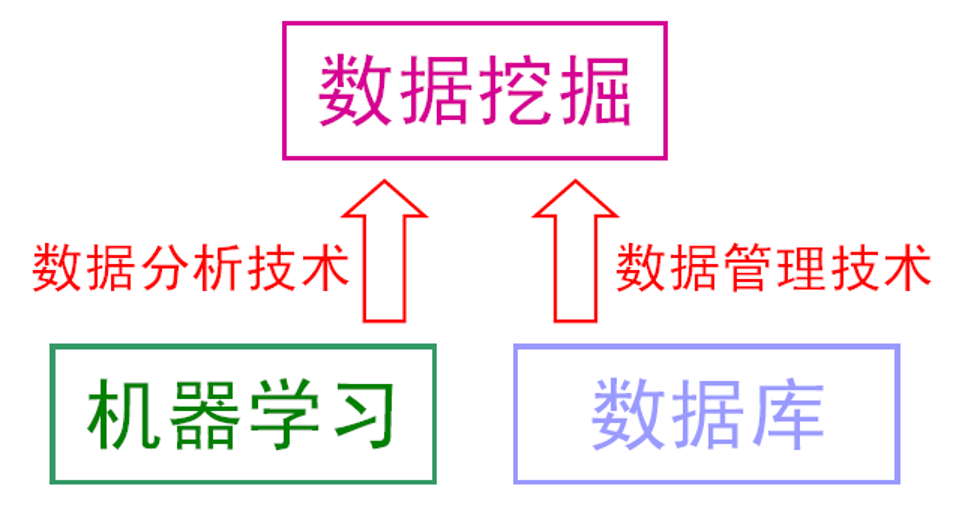
•机器学习是数据挖掘的重要工具。

•数据挖掘不仅仅要研究、拓展、应用一些机器学习方法，还要通过许多非机器学习技术解决数据仓储、大规模数据、数据噪音等等更为实际的问题。

•机器学习的涉及面更宽，常用在数据挖掘上的方法通常只是“从数据学习”，然则机器学习不仅仅可以用在数据挖掘上，一些机器学习的子领域甚至与数据挖掘关系不大，例如增强学习与自动控制等等。

•数据挖掘试图从海量数据中找出有用的知识。

•大体上看，数据挖掘可以视为机器学习和数据库的交叉，它主要利用机器学习界提供的技术来分析海量数据，利用数据库界提供的技术来管理海量数据。

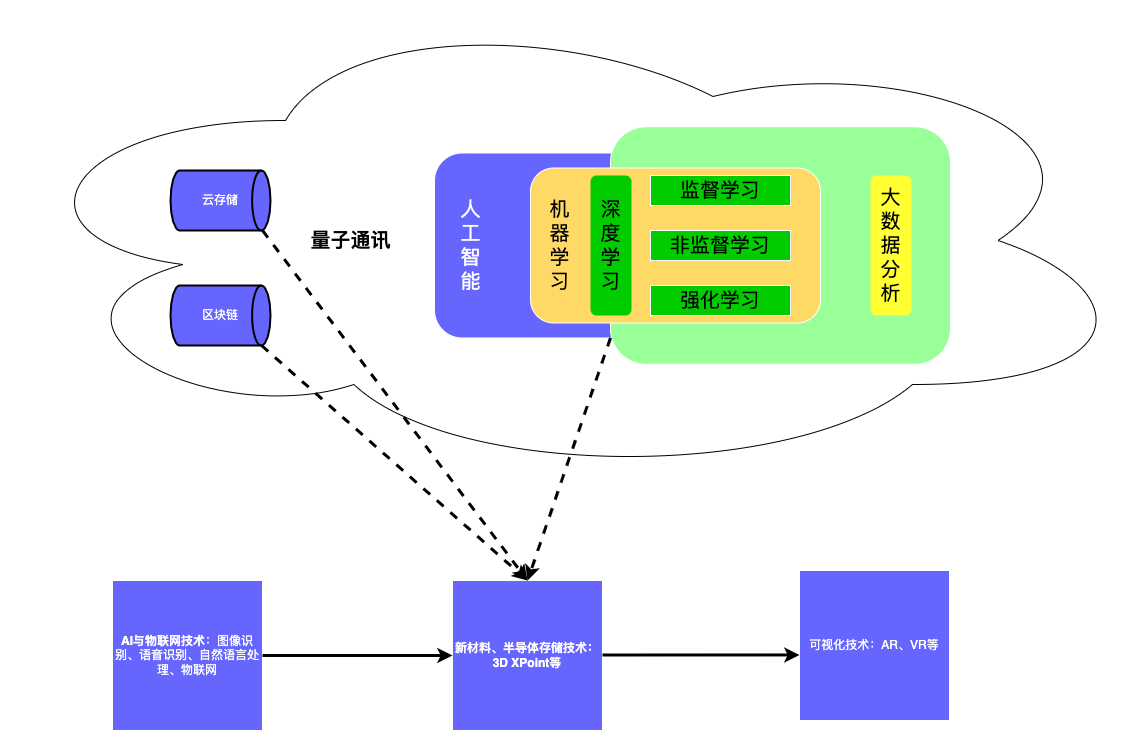
冯诺依曼机的现代观点：AI vs 大数据 vs 云计算

https://baike.baidu.com/item/3D%E7%A3%81%E5%AD%98%E5%82%A8%E5%99%A8/22383847

机器学习的三要素

机器学习=模型+策略+算法(优化算法)

[附件]

模型:决策函数、概率模型

在监督学习中，模型就是所要学习的条件概率分布或决策函数。
模型的假设空间F 包含所有可能的条件概率分布或决策函数。
假设空间可以是决策函数的集合

$$ F = {f |Y = f_\theta(X),\theta\in R^n $$

也可以是条件概率函数的集合

$$ F = {F | P_\theta(Y|X),\theta\in R^n $$

简单理解：

$Y= aX^2 +bX + c$

策略:选择模型的准则

资源：https://mp.weixin.qq.com/s/LN1X4TVgfF-FRhMlqEUVpw

损失函数：一次预测的好坏

0-1损失函数

$$ L(Y,f(X)) = \begin{cases} 1 &Y=f(X) \ 0 &Y{=}\mathllap{/,} f(X) \end{cases} $$

平方损失函数

$$ L(Y,f(X)) = (Y-f(X))^2 $$

绝对损失函数

$$ L(Y,f(X)) = |Y-f(X)| $$

对数损失函数

$$ L(Y,f(X)) = -logP(Y|X) $$

风险函数：平均意义下模型预测的好坏

经验风险最小化最优模型

$$ min_{\substack{f\in F}}\frac{1}{N}\sum_{i=1}L(y_i,f(x_i)) $$

算法:学习模型的具体算法

–解析解 –无解析解:数值计算

参考链接：https://zh.d2l.ai/chapter_optimization/index.html

梯度下降

梯度下降法的计算过程就是沿梯度下降的方向求解极小值，也可以沿梯度上升方向求解最大值。

$$ x \leftarrow x - \eta f’(x) $$

学习率（learning rate）决定目标函数能否收敛到局部最小值，以及何时收敛到最小值

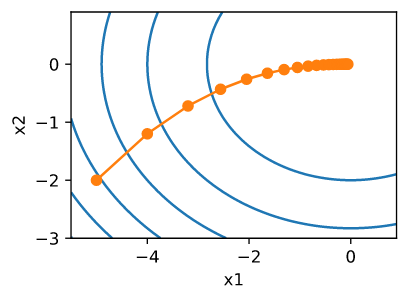
批量梯度下降：每进行1次参数更新，需要计算整个数据样本集
随机梯度下降：随机均匀选择一部分样本做梯度下降
小批量梯度下降法：随机选择一批样本

动量优化法

动量优化方法引入物理学中的动量思想，加速梯度下降，有Momentum和Nesterov两种算法。当我们将一个小球从山上滚下来，没有阻力时，它的动量会越来越大，但是如果遇到了阻力，速度就会变小，动量优化法就是借鉴此思想，使得梯度方向在不变的维度上，参数更新变快，梯度有所改变时，更新参数变慢，这样就能够加快收敛并且减少动荡。

$$ V_t \leftarrow \beta V_{t-1} + g_{t,t-1} $$

$$ X_t \leftarrow x_{t-1} - \eta_t V_t $$

自适应学习率优化算法

在机器学习中，学习率是一个非常重要的超参数，但是学习率是非常难确定的，虽然可以通过多次训练来确定合适的学习率，但是一般也不太确定多少次训练能够得到最优的学习率，玄学事件，对人为的经验要求比较高，所以是否存在一些策略自适应地调节学习率的大小，从而提高训练速度。

AdaGrad
RMSprop
Adadelta
Adam：Adaptive Moment Estimation

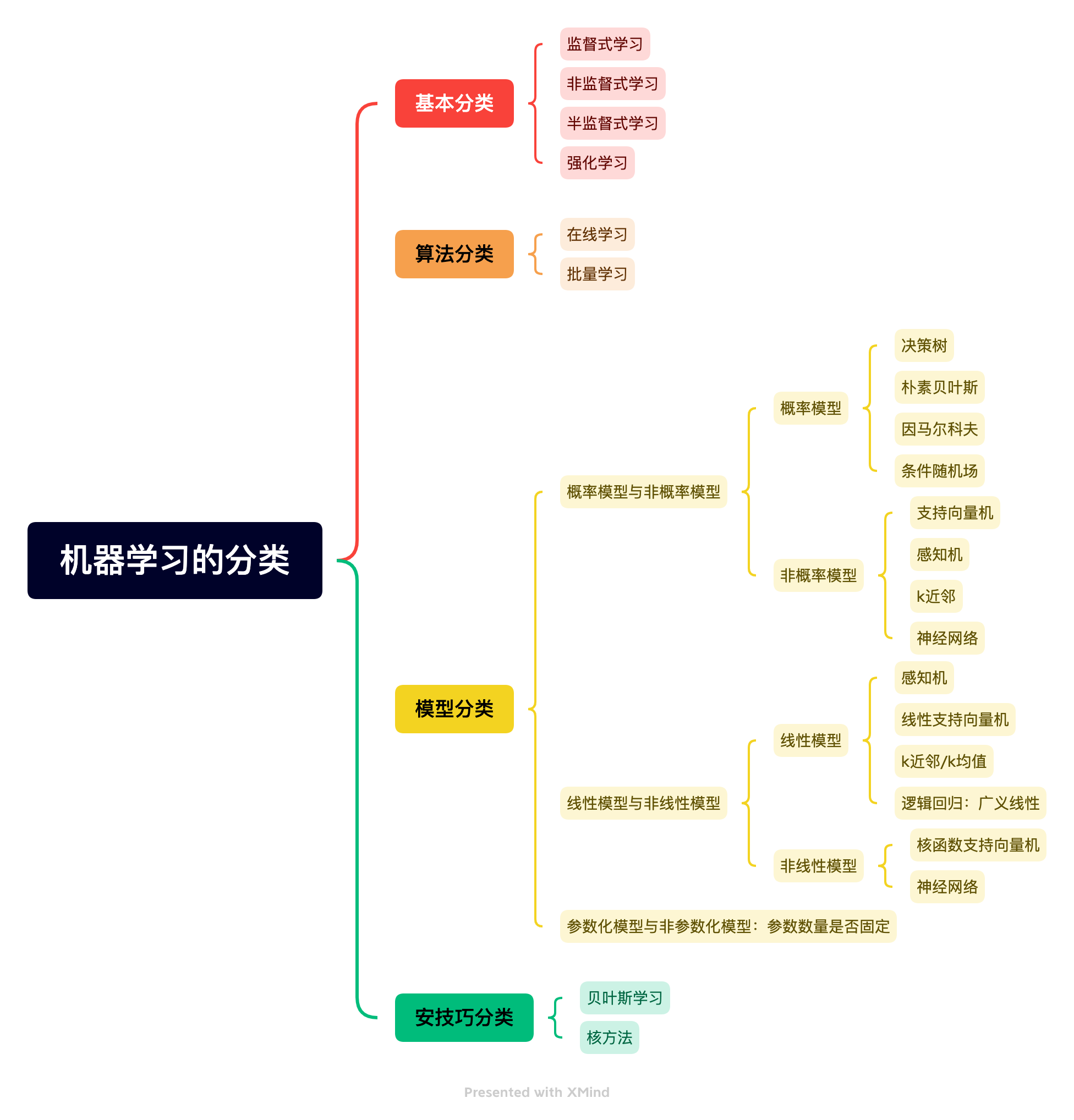
机器学习的分类

模型选择：正则化、交叉验证

选择模型的方法主要包括正则化、交叉验证

正则化：在经验风险上加一个正则化项(Regularizer)或罚项(Penalty term)。

一般形式：

$$ min_{\substack{f\in F}}\frac{1}{N}\sum_{i=1}L(y_i,f(x_i)) + \lambda J(f) $$

二阶形式：

$$ min_{\substack{f\in F}}\frac{1}{N}\sum_{i=1}L(y_i,f(x_i)) + \lambda||w|| $$

一阶形式：

$$ min_{\substack{f\in F}}\frac{1}{N}\sum_{i=1}L(y_i,f(x_i)) + \lambda||w|| $$

交叉验证：将数据分为训练集、验证集、测试集

简单交叉验证：训练集、测试集

S折交叉验证:S个互不相交的大小相同的子集，用S-1个子集训练模型